PARTIE 1: Evaluation des pertes de charges pour des debits donnés:

calcul point fonctionnement pompe dans les reseaux:

Mecaflux est ici utilisé pour étudier une installation de pompage.

Ce didacticiel correspond a un sujet de BTS choisi par un enseignant pour réaliser une activité de simulation Mecaflux avec ses élèves. Le sujet et son corrigé sont téléchargeables au format PDF : BTS 2009 sujet, BTS 2009 corrigé

Ce didacticiel détaillé est divisé en 3 PARTIES:

1. Evaluation des pertes de charges pour des debits donnés
2. Edition des courbes de pertes de charge sur une plage de débits donnée et recherche de points de fonctionnement d'une pompe.
3. Evaluation des puissances en fonction de la hauteur de dénivellé, des pertes de charge et du rendement de pompe

 

PARTIE 1: Evaluation des pertes de charges pour des debits donnés:

Mecaflux est un outil d'aide dont l' objectif est d' assister au quotidien le responsable de projet dans ses calculs les plus courants, alors que les questions du sujets sont clairement orientées vers le test des connaissances (ce qui est normal pour une épreuve d' examen). Nous verrons donc des approches pratiques d'utilisation du logiciel qui divergent de la méthode du sujet. Les methodes divergent sur l'utilisation par l'éxaminateur d'un polynome J = 0,076.Q2 + 0,26.Q qui permet une approche simplifiée de la perte de charge ammenant aux résulats.

 

Etudions les Données et reprennons les questions du sujet:(voir BTS 2009 sujet)

La figure 2 présente le profil de la conduite hydraulique reliant la pompe immergée du puits
L4 à la cuve R de la cuverie, destinée à recevoir l'eau de ce puits.
Il s'agit d'une conduite en PVC de diamètre intérieur D = 50 mm et de longueur totale
L = 920 m.

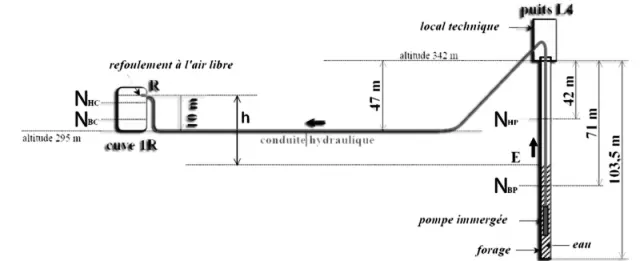
figure 2

Dans le sujet, Les pertes de charge linéiques le long de cette conduite dépendent du débit volumique Q et
sont données par :

J = 0,076.Q2 + 0,26.Q où J sont les pertes de charge POUR 100 m DE CONDUITE (elles sont exprimées en m de colonne d'eau). Q est le débit (exprimé en m3/h).

Notons ici , que cette formule de calcul de pertes de charge est une approximation n'integrant pas la rugosité, ni la viscosité. Ce polynome (J = 0,076.Q2 + 0,26.Q) est utilisé ensuite pour établir une relation entre le débit et la valeur Hpompe max.

Pour des raisons de compatibilité avec des cahiers des charges tres variés, Mecaflux calcule les pertes de charge d'apres la formule de Colebrook qui integre la rugosité et la viscosite du fluide, ceci amenera donc des différences entre les résultats produits par Mecaflux et BTS 2009 corrigé .

Vu la grande longueur et la forme de la conduite, on négligera les pertes de charge singulières devant les pertes de charge régulières.
Une prise d'air en haut du forage permet de maintenir la pression de la surface de l'eau dans le puits à la pression atmosphérique.
Côté refoulement dans la cuve 1R, l'eau débouche également à la pression atmosphérique.

Au cours d'une l'année, le niveau d'eau dans le puits peut varier entre une valeur minimale NBP et maximale NHP.

Questions et réponses:

A.1.1. Déterminer les valeurs hmin et hmax du dénivelé h entre le point de refoulement
dans la cuve R et la surface de l'eau dans le puits (voir figure 2) :
· hmin : valeur de h lorsque l'eau dans le puits est au niveau haut NHP
· hmax : valeur de h lorsque l'eau dans le puits est au niveau bas NBP.
les valeurs trouvées par lecture de la figure sont:

hmin = 42 – 47 + 10 = 5 m
hmax = 71 – 47 + 10 = 34 m

les questions relatives au théoreme de Bernoulli généralisé ne sont pas traitées ici (On pourra utiliser: Outils/ Application Bernoulli, du logiciel pour observer certains résultats de la relation)

L'examinateur etablit ici la relation Hpompe = 0,7. Q² + 2,4.Q + h en admetant que la perte de charge evolue suivant J = 0,076.Q² + 0,26.Q:

A.1.3 : DH = J.L/100 = (0,076.Q² + 0,26.Q).920 / 100 = 0,7. Q² + 2,4.Q avec Q en m3/h d'où Hpompe = 0,7. Q² + 2,4.Q + h

A.1.4. Compte tenu des caractéristiques de l'installation et des variations possibles du débit, calculer la valeur maximale de Hpompe.

Hpompe max est obtenu pour Q = Qmax = 10 m3/h et h = hmax = 34 m :
Hpompe max = 0,7.Qmax ² + 2,4.Qmax + hmax = 0,7x10² + 2,4x10 + 34 = 128 m

A.1.5. Calculer la puissance hydraulique Phydrau que doit fournir la pompe pour assurer un
débit Q = 10 m3.h-1 avec un dénivelé h = hmax.

Phydrau = Q. r.g. Hpompe max = (10/3600)x1000x9.81x128 = 3,49 kW

Ces resulats seront obtenu différement avec Mecaflux:

Hpompe max est obtenu en calculant la perte de charge pour

• Q = Qmax = 10 m3/h
• et h = hmax = 34 m :
• Données du calcul perte charge régulieres:
• Diametre= 50mm,
• debit = 10m3h ,
• Rugosité mm(selectionner autres matieres/pvc) = PVC= 0.007,
• fluide(viscosité) = eau à 10 degrés

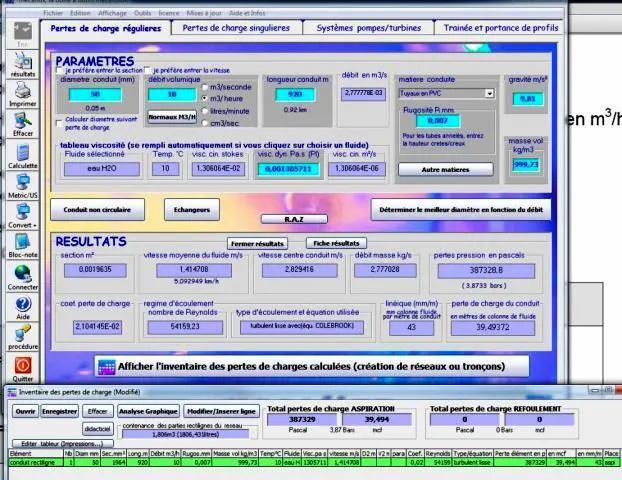
• La perte de charge calculée est de 39.5 metres.
• La valeur Hpompe est de 39.5 +34 = 73.5m pour le denivelé de 34 metres
• La valeur Hpompe est de 39.5 +5 = 43.5m pour le denivelé de 5 metres

nous procedons de meme maniere avec le debit de 4 m3h en modifiant juste la valeur de debit dans l'onglet pertes de charge régulieres:

• La perte de charge calculée est de 7.7 metres.
• La valeur Hpompe est de 7.7 +34 = 41.7 m pour le denivelé de 34 metres
• La valeur Hpompe est de 7.7 +5 = 12.7 m pour le denivelé de 5 metres

Nous constatons que ces valeurs sont largement inferieures au valeurs utilisant le polynome: J = 0,076.Q² + 0,26.Q. La formule de Colebrook est une référence en terme de précision, mais nous avons pu constater lors du calcul de pertes de charges, que le regime d'écoulement permet d'appliquer aussi la formule de Blasius ,nous pouvons tester et evaluer la différence de résultat en cliquant sur "Non":

 

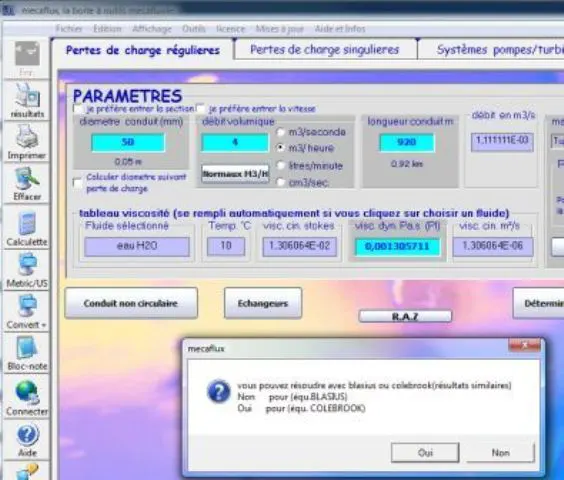
• Le resulat est 7.83 metres de pertes de charge pour le debit de 4 m3h.

Vu la grande longueur de la conduite, la précision de la formule utilisée pour le calcul des pertes de charge génere des resultats tres differents entre le polynome J = 0,076.Q² + 0,26.Q et l'utilisation des formules Colebrook ou Blasius.

La complexité de ces formules , et l'utilisation d'un ordinateur pour les résoudre rapidement, est justifiable par l'importance de ces différences.

 

Voyons maintenant comment choisir une pompe en fonction de ces données...