La formule se Poiseuille est utilisée pour évaluer le cœfficient de pertes de charge reguliere en écoulement laminaire

• écoulement laminaire: (R_e < 2000)
• Λ est le coefficient de pertes de charge régulières,
• Re est le nombre de Reynolds

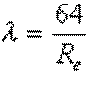
Λ=64/Re

Le logiciel de calcul de pertes de charge MECAFLUX, utilise La formule se Poiseuille pour déterminer le coefficient de perte de charge reguliere Λ pour les Nombre de reynolds< 2000

Calcul de perte de charge reguliere dans un conduit :

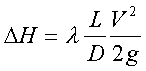
ΔH=Λ.(L/D).(V²/2.g)

• ΔH est la perte de charge en mètre colonne fluide
• Λ est le coefficient de perte de charge régulières
• V est la vitesse moyenne de l'écoulement
  D est le diamètre de l'écoulement
  L est la longueur de l'écoulement

Abaques de Moody:

L'equation de Colebrook-White utilsée pour tracer l'Abaque de Moody n'a pas de solution analytique, seul un calcul itératif permet de converger vers sa solution. Il faut donc utiliser un logiciel (comme le logiciel de calcul de pertes de charges Mecaflux) ou un abaque pour lire sa valeur en fonction du nombre de reynolds

Abaque de Colebrook, ou Abaque de Moody donne le coefficient de pertes de charges régulières (ordonnées gauche), en fonction du nombre de Reynolds (abscisses) et de la rugosité relative(ordonnées droite)

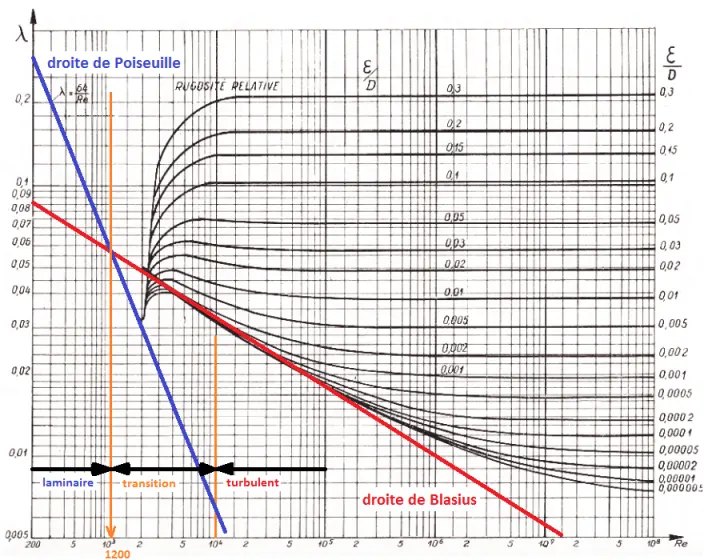
• Si Re < 2000 le régime est laminaire. On utilisera la formule de Poiseuille en écoulement laminaire pour trouver le cœfficient de pertes de charges ,
• si 2000<Re<3000 le régime est transitoire. (il peut basculer d'un état à l'autre il est bon de faire le calcul dans les deux états pour évaluer le comportement possible du fluide)
• si 2000 < Re< 10⁵ l'écoulement est turbulent lisse on utilisera la formule de Blasius en écoulement turbulent lisse pour trouver le cœfficient de pertes de charges ,
• si 2000 < Re l'écoulement est turbulent pour trouver le cœfficient de pertes de charges , nous utiliserons la formule Colebrook-White qui est utilisable dans tous les cas d'écoulement turbulent

Ces valeurs de Reynolds de transition sont des ordres de grandeur, les transitions se font progressivement et peuvent etre déclanchées par des irrégularités d'états de surface.

Voir Regime ecoulements